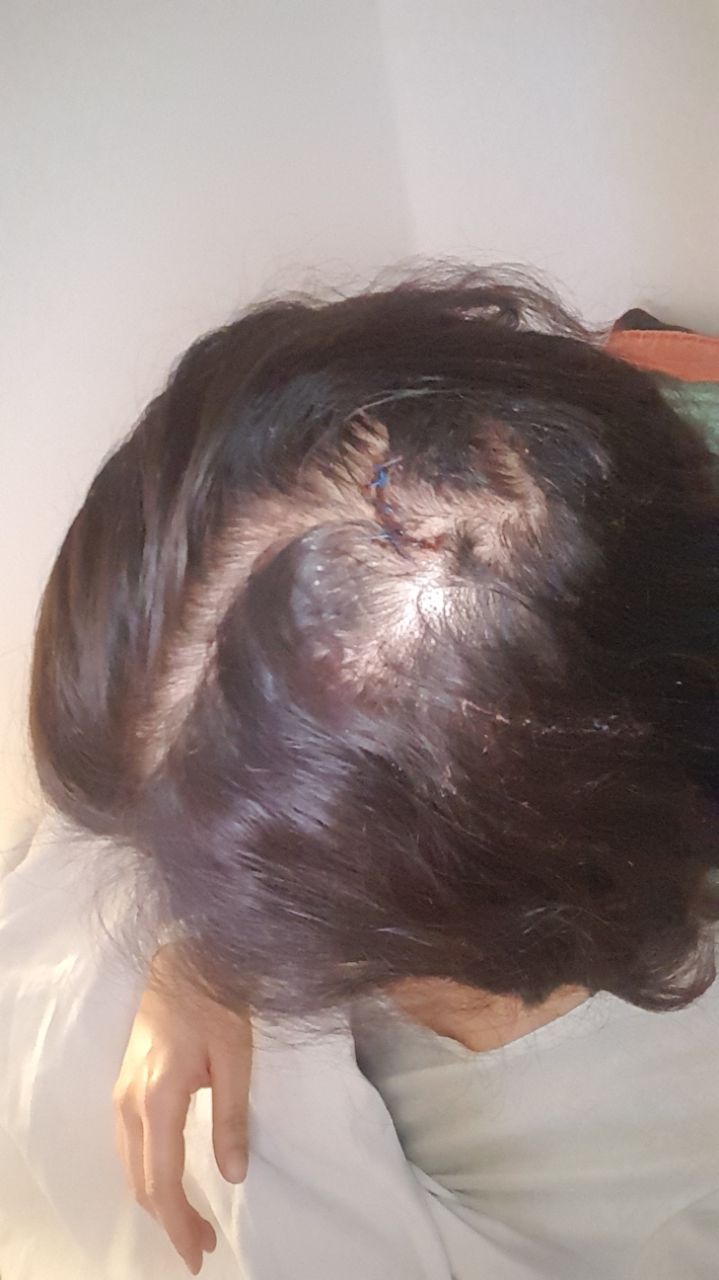
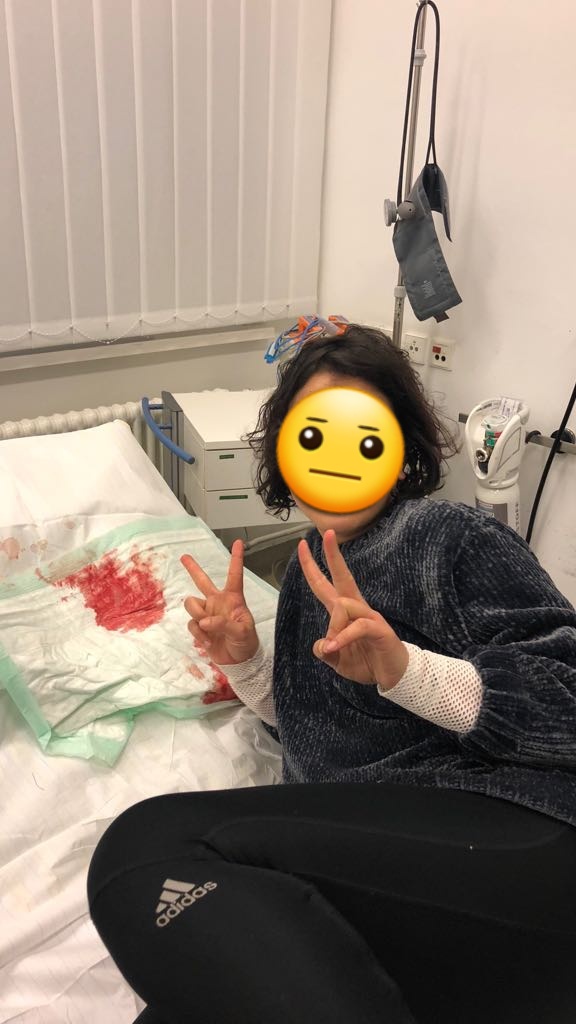
This new years eve a friend of mine was hit on the head by the debris of a rocket and had to spend the evening in the hospital. Being hit on the head seemed very unlikely to me, but how unlikely exactly? As a fan of the TheyDidTheMath subreddit I calculated how unlikely her new years eve was. It was also a great excuse to read up on probablity theory which I haven’t used since I graduated school 10 years ago.
tl;dr
It is pretty unlikely at circa 0.07 percent.
Rockets sold in Germany
As a starting point we take the number of rockets sold in Germany and expect all of them to be fired on new years eve. The expected sale of fireworks this year was 137,000,000€ of which 20% are rockets. Assuming an average price of 0.60€ per rocket this gives us:
\[rockets_{Germany} = 137000000 * 0.2 * 0.6 = 16440000\]Source: VPI - Verband der Pyrotechnischen Industrie (Association of the pyrotechnical industry)
Rockets in Berlin-Kreuzberg
My friend was hit on the head on a balcony in Berlin-Kreuzberg. Assuming the rockets are distributed evenly according to the population we can calculate the number of rockets in Kreuzberg as
\[rockets_{Kreuzberg} = \frac{rockets_{Germany}}{\frac{population_{Germany}}{population_{Kreuzberg}}}\]Filling in the current population numbers we get the number of rockets fired in Berlin-Kreuzberg on new years eve 2018.
\[rockets_{Kreuzberg} = \frac{16440000}{\frac{82670000}{153887}} = 30602\]Likelyhood of being hit on the head
We assume all debris from the rockets fired in Kreuzberg will also come back down on Kreuzberg. This should be reasonably close to the reality as most central Berlin districts have comparable population densities.
We assume an average hit area (\(area_{hit}\)) of \(0.25 m^2\). Due to the tumbling fall of the wooden sticks this should give a reasonable overlap with the head area viewed from above to ensure a hit.
Furthermore I expect my friend to have stayed outside until all rockets have been fired (pretty unlikely but estimating a firing frequency in dependency of the time is a can of worms I won’t open).
We take the basic formula for estimating the likelihood of a hit on the head from the excellent source What is the mathematical probability of getting pooped on by a pigeon in NYC?
\[1-(1-\frac{a}{A})^N\]and include our values
\[1-(1-\frac{area_{hit}}{area_{Kreuzberg}})^{rockets_{Kreuzberg}}\]which gives us
\[1-(1-\frac{0.25}{10380000})^{30602} = 0.000737\]The probability of being hit on the head be a falling rocket in Berlin-Kreuzberg is 0.000737 or circa 0.07 percent.
Aftermath
For those of you wondering what damage one of those puny little sticks can do. Turns out - quite a lot actually.